Trailer stability: The AST rule

As the author of articles in “Heavy Lift & Project Forwarding International” magazine Eager.one takes a closer look at the importance of elasticities with respect to transport stability. André van der Steen, our lead structural engineer at Eager.one, explains how this can help guarantee safe transport.

In trailer transports, the common practice rules – whereby the minimum tipping angle is 7 degrees – are not always sufficient. This is the case when elasticities are high, as this factor is not quantified by common practice rules.

As an example, Figure 1 shows a situation where the tipping angle is not exceeded by the ultimate loads plus the maximum uncompensated camber, also known as operational window. Whether the tipping angle is exceeded when taking elasticity into account can only be assessed when elastic deformation is actually calculated.

Figure 1: . The elastic rotation (red) relative to the tipping angle (grey); the actual safety is not quantified by common practise rules.

Therefore, the actual safety aspect of the tipping angle is not sufficiently acknowledged when using common practice rules. This point is also related to the rotational stiffness of trailer transports. Previous articles from Eager.one explained that stiffness of a trailer transport is k-m.g.H. (as indicated in figure 2).

Figure 2: Stability of trailer transports, elasticites are the common factor

For a more comprehensive and uniform assessment of the stiffness of a trailer transport, Eager.one developed the Available Stiffness Ratio (AST), which correlates the transport stiffness relative to the pendulum stiffness (denoted as m.g.H). The AST can be calculated using the following equation:

This ratio is vital in understanding whether a trailer is stable. Generally speaking, in order to generate a positive stiffness and be ‘potentially’ stable, the AST ratio must be positive; if the AST is negative, then so is the stiffness, meaning the trailer is unstable. For more robust safety calculations, a minimum value for the AST ratio can be determined. This will in turn assist safe transport operations.

Elasticity should also be considered here: to find a clear boundary for the required stiffness of a trailer transport, the elastic rotation (roll) must be smaller than the allowable elastic rotation (see figure 1).

Taking all of that into account leads to the following equation (see figure 2):

Whereby:

• S is the sideward ratio, determined using the following calculation:
  
• F is the forward ratio, determined by:
  
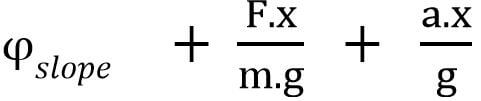
• The tipping angle of the transport is represented by:
  
• The steepness tipping line (in horizontal plane) is shown as β and calculated using:
  

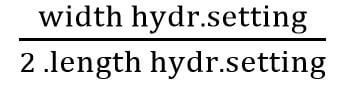
Essentially, the tipping angle, minus the sideward ratio, minus the steepness and forward ratio should be larger than sideward ratio divided by the AST.

Eager.one has tested this rule and upon comparing the outcome with dedicated simulations, the results are accurate. Therefore Eager.one is confident that this is a very reliable rule for the future trailer stability calculations. It will enable unstable trailer transports to be recognized.

For a more comprehensive and uniform assessment of the stiffness of a trailer transport, Eager.one developed the Available Stiffness Ratio (AST).

To put this rule into perspective, the equation will be illustrated with a real-world example. We will look once again at an accident where an SPMT combination tipped during a ro-ro operation when crossing ramps connecting a barge to the quay.

The accident

The load was being moved on 14 axle single-line SPMTs in a 10,9,9 configuration – in a triangular hydraulic layout. It had a total load of 378 tons, including power pack units, and a center of gravity of 2.1 m above deck (3.1 m above pivots). The steepness tipping line (ß) was 7.3 percent (in horizontal plane).

Other details about the move included:

• Base stiffness, solid ground: k = 381 kNm/deg
• Base stiffness, ro-ro to barge: k = 211 kNm/deg
• Standing pendulum stiffness: g.H = 221 kNm/deg

Prior to the calculations, values for the environmental influences and the operational window must be set:

• Uncompensated camber: 2 degrees + (50 percent safety) = 3 degrees (5.25 percent)
• Uncompensated slope: 2 degrees + (50 percent safety) = 3 degrees (5.25 percent)
• Wind acting sideward: Fy/mg (sufficient for low area/mass ratio) = 1 percent
• Acceleration (cornering): (ay/g) , ay=0.075ms-2 | 0.75 percent sideward
• Deceleration (braking): (ax/g) , ax=2ms-2 | 20 percent forward.

Taking those details into account, the sideward and forward ratios can be determined, according to the formulas laid out above:

S = 5.25 percent + 1 percent + 0.75 percent = 7 percent
F = 5.25 percent + 20 percent = 25.25 percent

As the steepness tipping line was 7.3 percent, we know that ß.F = 1.86 percent.

With the figures in place, the stability can be calculated for four situations using the equation:

The situations A and B describe the route of the fatal accident, while situations C and D describe a four-point (4p) hydraulic set up as an alternative.

A.   Solid ground in a three-point (3p) hydraulic layout, with a tipping angle of 8.6 degrees (15 percent):

Therefore:

As this (9.7<6.14) is not true and the calculation deems this move unsafe.

B.   Ro-ro to barge operation in a 3p hydraulic layout with a tipping angle of 8.6 degrees (15 percent):

As the AST is negative, the trailer transport is fundamentally unstable. As a consequence, the trailer actually tipped.

Eager.one is confident that this is a very reliable rule for future stability calculations. It will enable unstable trailer transports to be recognized.

For the following two scenarios, a 4p hydraulic layout in a 7,7,7,7 configuration has been simulated. In this case, the base stiffness (k) on solid ground is 561 kNm/deg. The base stiffness (k) on ro-ro to barge in this layout is 363 kNm/deg.

C.   Solid ground in a 4p hydraulic layout, with a tipping angle of 4 degrees (23 percent):

Therefore:

As this (5<16) is true, the calculation deems this move is very safe.

D.   Ro-ro to barge operation in a 4p hydraulic layout, with a tipping angle of 13.4 degrees (23 percent):

Therefore:

As this (10.9<16) is true, the calculation deems this move is also safe.

In both 4p scenarios, C and D, the safety calculations deemed the move stable.

Following this AST rule would have resulted in both 3p hydraulic layouts not being executed. Further still, since the AST ratio in situation B – the actual accident conditions – was below 1 (-0.04), this method of assessing trailer stability would have deemed this operation fundamentally unstable. When looking at these calculations, it shows that an accident was inevitable when executing the move in those conditions.

However, this AST rule works, there is one drawback; although pendulum stiffness (m.g.H) can easily be calculated by most operators, the determination of the base stiffness (k) is more difficult. Two solutions can solve this:

• The development of a tool for the market capable of calculating the k value for any transport;
• Or the establishment of some standardized, minimum values for k for typical situations that can be adopted market wide.

Eager.one plans to come up with a proposition in a future article.

The content of this article is intended to provide a general guide to the subject matter. Specialist advice should be sought about your specific circumstances.

Read more about Trailer Stability

This article is the final article in a series of 3. Here you can find the links to article 1 and 2:

1. Stability of SPMTs: Common practice and safety
2. Calculating how to ensure transport stability

Next to these articles, we have also organized a webinar about this subject. The recording of this webinar is still available to watch. Click here for more information.