Calculating how to ensure transport stability

As the author of articles in the “Heavy Lift & Project Forwarding International” magazine, André van der Steen, lead structural engineer at Eager.one, explains calculations on how to ensure transport stability. 

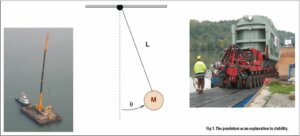
Many of us will be able to recall one of our first physics lessons, where a pendulum swings across the science laboratory. Knowing how a pendulum behaves is an important step towards understanding all types of motion, including what affects stability during heavy transport.

In earlier articles from Eager.one, the importance of elasticities when it comes to stability has been explained. Although this is quite evident for the expert, it can be hard for the uninitiated to recognize elasticities.

A practical understanding is helpful for anyone involved in heavy and oversize cargo transportation. Many stability issues, like the tipping of barges or trailers, can be explained in layman’s terms using the pendulum.

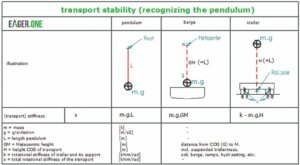
For a barge or trailer transport, the pendulum can be identified using the formula shown in Figure 2. The length of the pendulum for barges is the well-known GM value (metacentric height). But how can you identify the pendulum for trailers?

The pendulum for a trailer is positioned upside down; in other words, it has a negative pendulum length. Such a system has a negative stiffness and is unstable. A trailer generates positive stiffness due to its chassis and its support (such as soil, ramps, etc). This number must be higher than the negative stiffness of the pendulum in order for the trailer to be stable. This leads to the following indications for stability, for barges and trailers:

• For barges, the overall stiffness of the transport is m.g.GM. In order to generate a positive stiffness, the GM value must be larger than zero.
• For trailers, the overall stiffness of the transport is k-m.g.H. In order to generate a positive stiffness, the ‘base’ stiffness (k) must be larger than the (standing) pendulum stiffness m.g.H.

We know that in some accidents these two aspects were not respected, leading to an inevitable catastrophe. In most cases, the crash was a result of the following factors:

• For barges, when the GM drops suddenly due to the lifting of heavy objects on board.
• For trailers, when suddenly, the ‘base’ stiffness (k) drops due to the crossing of elasticities (example: ro-ro ramps).

In order to generate a uniform variable to identify the stiffness of a trailer transport, Eager.one has introduced its Available Stiffness of Transport (AST) ratio, which correlates the transport stiffness relative to the pendulum stiffness mgH.

Available Stiffness of Transport

AST = (k-m.g.H)/m.g.H

The following examples of AST values give an interpretation to the transport stiffness:

Example:

The equation is best illustrated with a real-world example. Recently, an SPMT combination tipped during a ro-ro operation when crossing ramps connecting a barge to the quay. The transport is defined as follows:

• A 14 axle single-line SPMT combination in a 10,9,9 configuration (triangular hydraulic layout)
• Total load (including. Power pack unit, excluding trailer): 378 tons • Centre of gravity at 2.1 m above deck (3.1 m above pivots)
• Base stiffness, solid ground (3p layout): k = 381 kNm/deg
• Base stiffness, ro-ro to barge (3p layout): k = 211 kNm/deg
• ‘Standing’ pendulum stiffness m.g.H = 221 kNm/deg

From the above it can be concluded:

• AST ratio solid ground (381-221)/221 = 0.72
• AST ratio ro-ro = (211-221)/221 = -0.04

For solid ground, the AST ratio of 0.72 is sufficient to withstand environmental influences (camber, wind, cornering, breaking, etc.) without tipping. However, at the moment the trailer crosses the ro-ro ramps the AST ratio drops to -0.04 and is unstable. The transport must go wrong, and that is what happened. The transport tipped causing millions of euros-worth of damage.

Interesting side notes:

• The ‘common practice’ minimum tipping angle of 7 degrees was respected with a value of 8.4 deg.
• A four-point layout (7,7,7,7) in a ro-ro operation has a base stiffness of 363kNm/deg and an AST ratio of 0.64, so is much more suitable.

It is imperative that the AST ratio remains positive during heavy transportation projects. How to determine the allowable AST value for a safe operation will be explained in Eager.one’s next article, which will be published in our August/September edition.

The AST ratio is somewhat comparable to the variable GM (metacentric distance) for barges. We know that GM must be positive. However, setting an actual limiting value, in order to have a safe barge, is a little more complicated.

The content of this article is intended to provide a general guide to the subject matter. Please contact us for specialist advice about your specific circumstances.

This article was also published in the May/June 2020 edition of HLPFI magazine. Read the online version here.

This is the second article in a series about transport stability. You can find the first article “Stability of SPMTs: Common practice and safety” here.